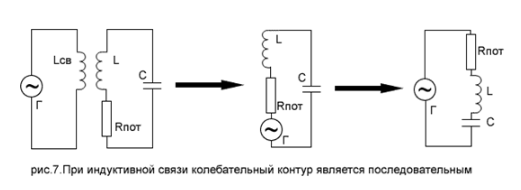
In aseries resonantcircuit, the generator is connected in series with the coil and capacitor. For example, in the case of inductive coupling, the resonant circuit is continuous because an electromotive force is induced in the coil, which is equivalent to connecting the generator in series with coil L and capacitor C. The figure shows the equivalent relationship of these transformations.

During resonance, a series circuit has the following characteristics:

1. The minimum loop resistance is equal to Rpot.

2.The voltage across the capacitor (or coil) is Q times the voltage of the generator. Q is the quality factor of the circuit.

3. The maximum and equal current flowing through the circuit

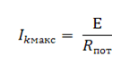
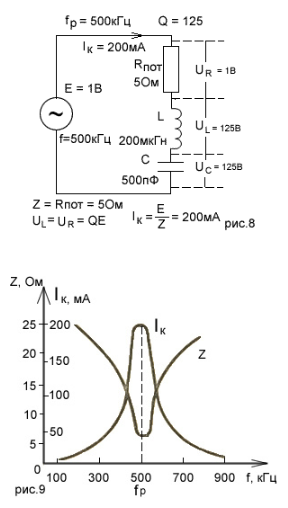
The diagram illustrates a specific example of a series resonant circuit, and Figure 9 shows its frequency characteristics, provided that the internal resistance of the generator is small.

Therefore, voltage resonance occurs in aseries resonantcircuit. For undeveloped circuits containing series connected inductive, capacitive, and resistive elements, voltage resonance is a characteristic.

The name voltage resonance reflects the equality of the effective voltage values on capacitive and inductive components with opposite phases.

The physical reason for the increase in voltage is the fluctuation of a large amount of energy stored alternately in the capacitive electric field and the inductive element magnetic field. Through voltage resonance, a small amount of energy from the energy source compensates for the energy loss in the active resistor, which is sufficient to maintain continuous resonance in a system with relatively large amounts of magnetic and electric field energy.